Factorise X 4 4 3x 2 Dronstudy Questions Find All The Other Zeros Of The Polynomial X4 X3 9x2 3x 18 If The Solve For X In This Complex Equation X 4 3x 2 4 0 Youtube Ex 2 4 2 Use The Factor Theorem To Determine Whether Ex 2 4 how do you factorise?X^44/x^41 factorise Get the answers you need, now!
Factor X 4 X 2 Problem With Solution Lunlun Com
X^4+4/x^4 factorise
X^4+4/x^4 factorise-Jun 22,21 Factorise 3x^2 x 4?Factorisex28x16 x28x16=x22×x×442=x72 Ans Please scroll down to see the correct answer and solution guide



Factorise X4 X2 1 Polynomials Maths Class 9
Factorise completely ( x − 4x^3) (x4x 3) = x (14x 2 ) Just taking a factor of x out of both terms Within the inner bracket we have a difference of two squares 1 2 =1 and (2x) 2 =4x 2 therefore we can write x (14x 2) = x (12x) (12x) Answered by Edward C • Maths tutorThis is the same as x 2 0x 4, so you need to find factors of 4 that add up to 0At first glance, this does not appear to be a quadratic — and, in technical terms, it isn't But this expression is quadratic in form, meaning that it can be restated as a quadratic, it follows the same patterns, and it can be factored by using the same techniques
Factor x^41 x4 − 1 x 4 1 Rewrite x4 x 4 as (x2)2 ( x 2) 2 (x2)2 −1 ( x 2) 2 1 Rewrite 1 1 as 12 1 2 (x2)2 −12 ( x 2) 2 1 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = x2 a = x 2 and b = 1 b = 1 (x2 1)(x2 −1) ( x 2To multiply powers of the same base, add their exponents Add 4 and 4 to get 8 Subtract 194x^ {4} from both sides Subtract 1 9 4 x 4 from both sides Substitute t for x^ {4} Substitute t for x 4 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {Factorise x^2 4x5 Get the answer to this question by visiting BYJU'S Q&A Forum
Evey123 evey123 Math Secondary School answered X^44/x^41 factorise 2 See answers Factorise x4 x2 1 Factorise x4 x2 1 how_to_reg Follow thumb_up Like (11) visibility Views (712K) edit Answer question_answer Answers(2) edit Answer person Kishore Kumar Consider x 4 x 2 1 = (x 4 2x 2 1) – x 2 = (x 2) 2 2x 2 1 – x 2 = x 2 1 2 – x 2 It is in the form of (a 2 – b 2) = (a b)(aMéthode pour réussir sa factorisation à tous les coups 1) Compter le nombre de termes (un terme est un « truc » séparé par un signe ou ) ex dans 3x^2 5x il y 2 termes 2) Repérer un facteur commun (un «truc» qui peut être un x, un nombre ou une parenthèse, et qui est commun à chacun des termes) ex dans 3x^2 5x = 3



Www Pearson Com Content Dam One Dot Com One Dot Com International Schools Pdfs Secondary Curriculum International Old Maths Ial Pure Maths 2 Sb Pdf




3 Nsc Common Test March Question 1 1 Factori Gauthmath
Factor x^24 x2 − 4 x 2 4 Rewrite 4 4 as 22 2 2 x2 − 22 x 2 2 2 Since both terms are perfect squares, factor using the difference of squares formula, a2 −b2 = (ab)(a−b) a 2 b 2 = ( a b) ( a b) where a = x a = x and b = 2 b = 2 (x2)(x− 2) ( x 2) ( x 2) There are only a few values of a, c, p, r that satisfy the first two equations After some guessing and checking (kind of like the guessing and checking that goes into factoring a quadratic**), we find that 64 x 4 64 x 3 − x 2 − 51 x 39 = ( 4 x 2 3 x − 3) ( 16 x 2 4 x − 13) And you can finish by solving the two quadraticsSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Ex 14 2 4 Iii Factorise X 4 Y Z 4 Chapter 14 Class 8




Factor Completely X 2 412 4x 2 41 96 Select One Chegg Com
Du sur les forums de jeuxvideocomFor example putting 2x² x 3 into the form (2x 3)(x 1) factorise 9x to the power of 4 64y to the power of 2 Math Factorise X'29X 14 maths factorise a^7ab^6 You can view more similar questions or ask a new question Transcript Ex 24, 4 Factorise 12x2 7x 1 12x2 7x 1 We factorize using the splitting the middle term method = 12x2 4x 3x 1 = 4x (3x 1) 1 (3x 1) = (3x 1) (4x 1) Ex 24, 4 Factorise (ii) 2x2 7x 3 2x2 7x 3 We factorize using the splitting the middle term method = 2x2 6x x 3 = 2x (x 3) 1 (x 3) = (x 3) (2x 1) Ex 24, 4 Factorise (iii) 6x2 5x 6 6x2 5x 6 We




Online Factoriser With Steps



1
(xy)(xy)(x^2y^2) Expression =x^4y^4 Recall the factorization of the difference of two squares a^2b^2 = (ab)(ab) In our example, we will use this factorization twice Note x^4 =(x^2)^2 and y^4 =(y^2)^2 Applying the factorization above Expression = (x^2y^2)(x^2y^2) Now, the second factor above is also the difference of two squaresFactor x 4 – 2x 2 – 8;Thus \(x^22y^22xy=0\) doesn't have any real solutions if \(y\ne0\), and so we can't factorise the first bracket any further For the second bracket, the discriminant is also \ (2y)^24(2y^2)=4y^2, \ and so we can't factorise the second bracket either Therefore we've fully factorised \(x^44y^4



View Question Factorise Fully X 2 16 X 4 3x 5




Form 4 Quadratic
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Factorise `x^4x^225` Ex 24, 5 Chapter 2 Class 9 Polynomials Last updated at by TeachooThis is similar to other factorisation problems such as x 2 5x 6 In this problem, you would find prime factors of 6 that add up to 5 (In this case 3, 2) Now, do the exact same with this problem!




3rdmath Flip Book Pages 251 287 Pubhtml5




Factorise X 4y 4 Xy Maths Questions
Show that \ (x^22y^2)^24x^2y^2=x^44y^4, \ and hence factorise \(x^44y^4\) Previous Next UCLES O level Mathematics Alternative A Algebra, QP 411/3, 1963, Q5(i) Question reproduced by kind permission of Cambridge Assessment Group ArchivesGet answer Factorise `x^(4) x^(3) x^(2) x` factorise x 4 4x 2 16 Share with your friends Share 0 (X 2) 2 2(X 2)(4)(4 2) =(X 2 4) 2 it might be 8X 2 instead of 4X 2 2 ;




Algebra Assessment Solutions Algebra And




3 Ways To Factor Trinomials Wikihow
Click here👆to get an answer to your question ️ Factorise x^4 3x^2 2Get answer Factorise (a) x^(4)4x^(2)16 " " (ii) x^(4)4 Apne doubts clear karein ab Whatsapp par bhi Try it nowEduRev Class 10 Question is disucussed on EduRev Study Group by 115 Class 10 Students




Rd Sharma Solutions For Class 8 Chapter 7 Factorization Download Free Pdf




Factorize X 4 4 Maths Factorization Of Algebraic Expressions Meritnation Com
Factorise X^4 3X 2 Created by Rajesh76bus Math geetaranipatnayak Stepbystep explanation Because the x 4 coefficient is 1View Full Answer here it is only 4x 2 not 8x 2 0 (x 2 2xy)(x 2 2xy)(12) 0 Hope this helps!!!1 ;∵ x4 (y z)4 = x22 (y z)22 = (x2) (y z)2 (x2) (y z)2 Using a2 b2 = (ab)(ab)We can factorise x2 (y z)2 further as x2 (y z)2




Find The Roots Of 2x 2 X 4 0 By Quadratic Formula



Q Tbn And9gcshl5gqvyaxdjxfuypwzss8ohr9maslpl Txedxxca5dgzd6p Usqp Cau
Aryan Raj, added an answer, on 23/9/ Aryan Raj answered this Factorisr Was this answer helpful?Check x 4 is the square of x 2 Check y 4 is the square of y 2 Factorization is (x 2 y 2) • (x 2 y 2) Trying to factor as a Difference of Squares 12 Factoring x 2 y 2 Check x 2 is the square of x 1 Check y 2 is the square of y 1X^4 324 (x^2)^2 18^2 That would be a perfect square if the term that is twice the product of the square roots of those two terms were added That's 2·18·x^2 or 36x^2 So we add that between those terms and then subtract it That's the same as adding 0 (x^2)^2 36x^2 18^2 36x^2




Factors Learning Outcomes Ppt Download




Factorise X 2 4x 4
I am trying to factor x 4 1 in to two multiplied polynomials Homework Equations My teacher gave us this hint that its factored form is (ax2bxc)(ax2bxc) The Attempt at a Solution First i assumed that a and c were equal to 1 so that when x 2 is multiplied by the other x 2 is gives me x 4 and 1 times 1 gives me 1Step by step solution Step 1 Trying to factor as a Difference of Squares 11 Factoring x 44 Theory A difference of two perfect squares, A 2 B 2 can be factored into (AB) • (AB) Proof (AB) • (AB) = A 2 AB BA B 2 = A 2 AB AB B 2 = A 2 B 2 Note AB = BA is the commutative property of multiplication Note AB AB equals zero and is therefore eliminatedFactorise `(a) x^(4)4x^(2)16 " " (ii) x^(4)4`



Factor X 4 X 2 Problem With Solution Lunlun Com
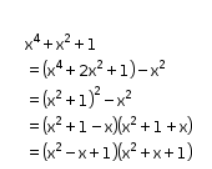



Factorise X4 X2 1 Home Work Help Learn Cbse Forum
Factorise x^4/44/x^41, by a^2b^2Click here👆to get an answer to your question ️ Factorise x^44 4x^4 1Page 2 Topic Comment factoriser x^4 4 ?




X4 X Z 4 Factorize Than Using Identity B2 Brainly In




Ex 14 2 4 Iv Factorise X 4 X Z 4 Chapter 14 Class 8
Return to x x 2 = 2 ± 2 i 3 So, we can now convert x 4 4 x 2 16 into factors x 4 4 x 2 16 = ( x 2 − 2 2 i 3) ( x 2 − 2 − 2 i 3) Repeat quadratic formula for each factor x l e f t = 0 ± 0 2 − 4 ( 1) ( 2 2 i 3) 2 x l e f t = ± − 8 − 8 i 3 2 x r i g h t = 0 ± 0 2 − 4 ( 1) ( 2 − 2 i 3) 2 a non c'est puissance 4 ou fois 4 ?To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Factorise `x^4x^2y^2y^4`



How To Factorise 16x 4 Y 4 Quora



Factorise X4 X2 1 Polynomials Maths Class 9
Re Factorisation de X^41 Il faut factoriser dans les deux polynômes (X 2 i) et (X 2 i) Pour ce faire, il faut calculer les "racines" de i et i qui sont en regroupant correctement tes 4 facteurs du premier degré (à coefficient dans ) en deux groupes de 2, tu obtiendras deux facteurs du second degré à coefficient dans1 Krittika Pramanik, added an answer, onDegree of the given equation is 2 So given equation is a quadratic equation(Degree of a polynomial Wikipedia) So equation can be written in the form of (xa)*(xb) Where (xa),(xb) are factors of the equation So by expanding we get x^2(ab



Http Www Ma Man Ac Uk Mdc Math101 Notespermanant What you need ans factor Pdf




Why Is X 4 16 When Factored Not Just X 2 4 X 2 4 Brainly Com
Yes, the four solutions to x^44=0 are x=±1±i So to factor this completely, you have x^44=(x1i)(x1i)(x1i)(x1i) If you multiply the first two factors and the second two factors, you obtain x^44=(x^22x2)(x^2–2x2) Alternatively, if you multiply the first and last factor, and also the second and third, you get x^44=(x^2–2iGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Factorising Quadratic Expressions 1




Factorise X 4 X Z 4 Brainly In
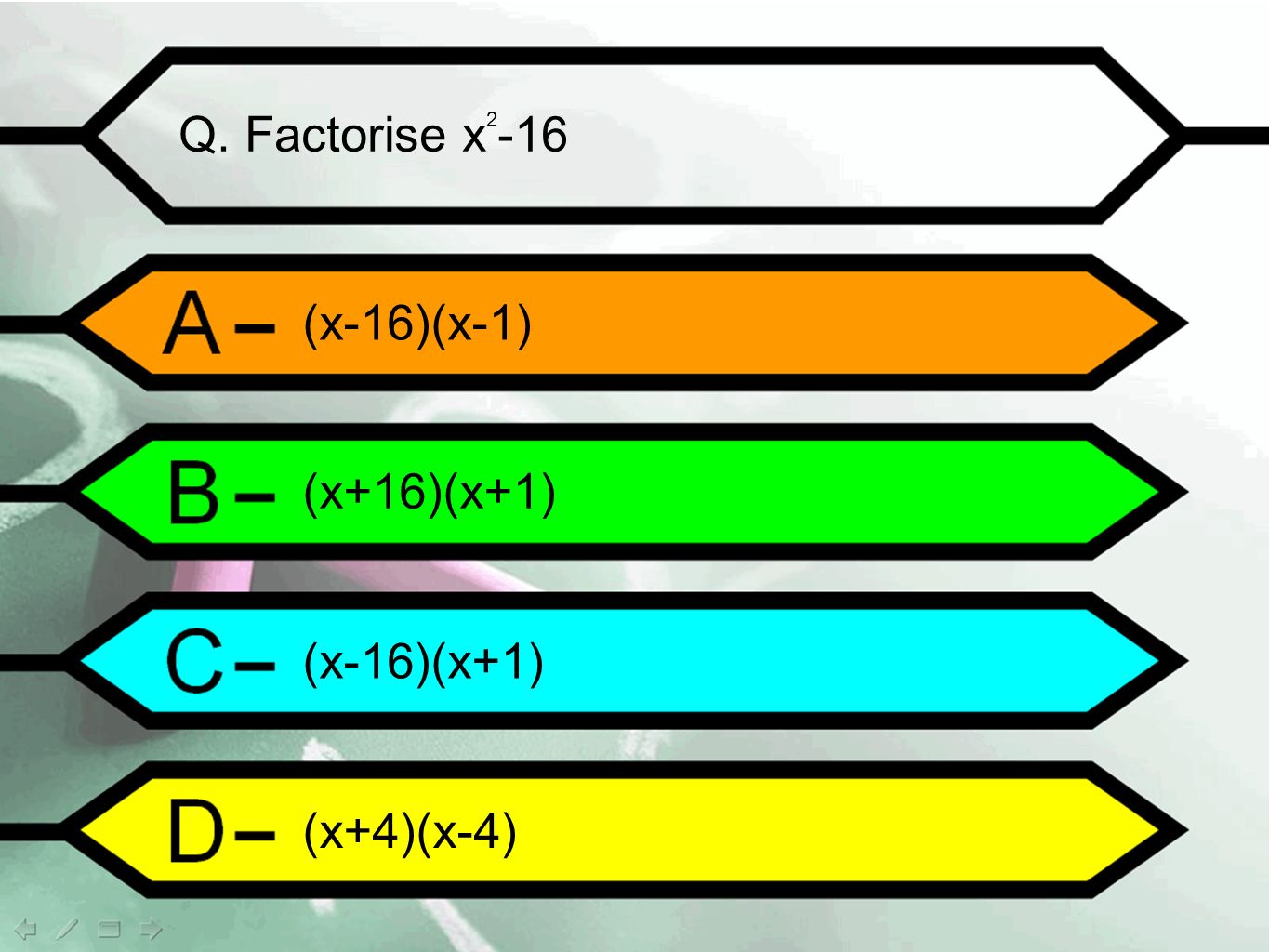



Q A Quadratic Equation Is An Equation With 1 Solution An Equation With 2 Solutions An Equation With 0 Solutions An Equation With 3 Solutions Ppt Download




Factoring Calculator Wolfram Alpha




Factor Algebraic Expression X 2 X 4 X 4 X Youtube
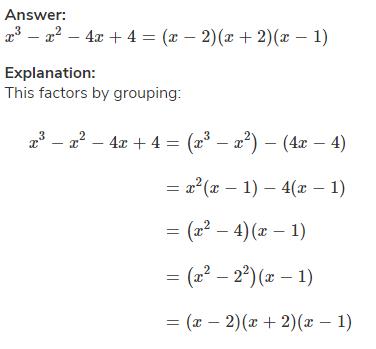



X 3 X 2 4x 4 Factorise Edurev Class 9 Question



Factorisation




Factorise X 4 X 2 25 Youtube




How To Factorise A Polynomial By Splitting The Middle Term A Plus Topper



Factorize X 4y 4 Xy Sarthaks Econnect Largest Online Education Community
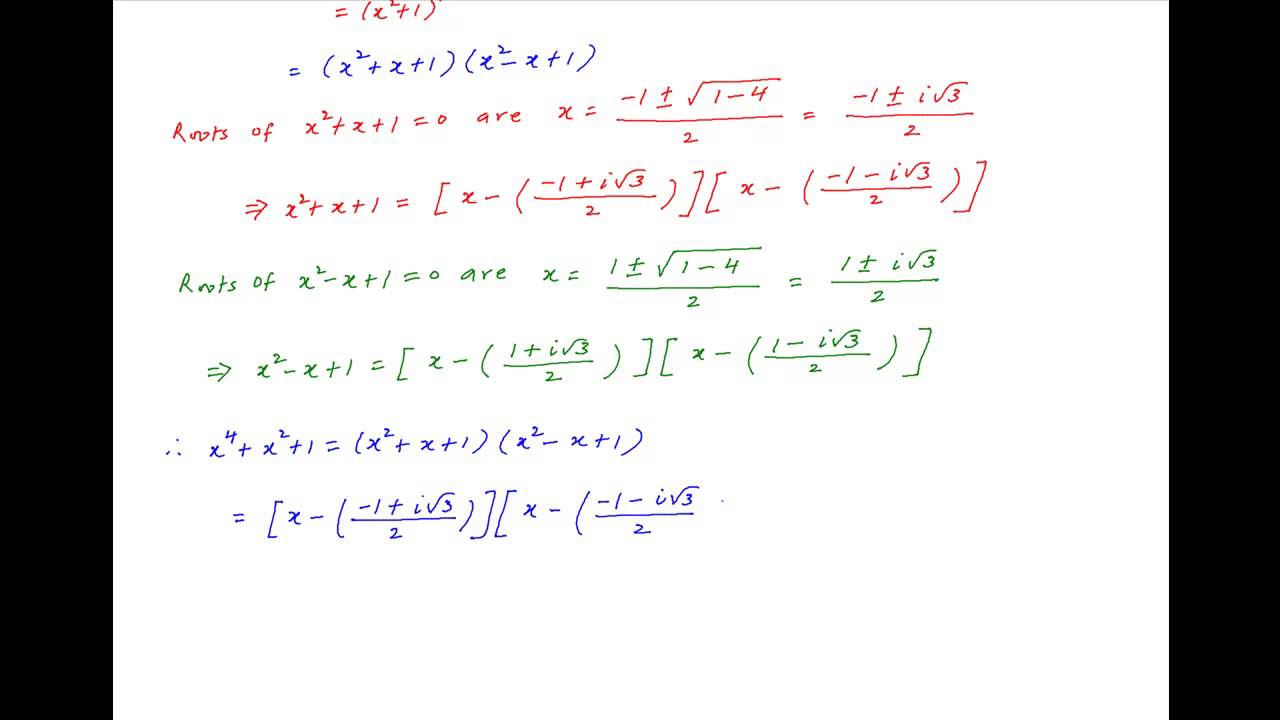



Factorize X 4 X 2 1 Into Linear Polynomials Youtube



Factorisation




Factorise X 4 X 2 1




Quadratic Equations That Factorise




X Power 4 Plus 4 Factorise Its Answer Is X Power 2 Plus 2x Plus 2 X Power 2 Minus 2x Plus 2 Brainly In




Factorise X2 X 4 1 8 Mathematics Topperlearning Com 057ly522




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Q Tbn And9gct1wipzbe8ag2bz7jujc N4 D 4q6i17kqhgvmu6mq Cpiepjar Usqp Cau



Http 2fv5d843v9w22sxtto1ibxtu Wpengine Netdna Cdn Com Wp Content Uploads 15 12 Algebra H Factorising Expanding Solving Polynomials V2 Solutions Pdf



Factorise X 4 1 X 4 1 Draw Cheerio



Factorization Of Algebraic Expressions Identities Examples Cuemath




Rd Sharma Class 9 Chapter 5 Factorization Of Algebraic Expressions




Algebra Expansion And Factorisation Pdf Free Download



Factorise X 2 3x 4




Online Factoriser With Steps




Using The Factor Theorem Show That X 2 Is A Factor Of X 3 X 2 4 X 4 Hence Factorise The Polynomial Completely Mathematics Shaalaa Com




Using Factors Theorem Factories X 4 X 3 7x 3 X 6




Ex 14 2 1 V Factorise 4x 2 8x 4 Chapter 14 Class 8



Using Factor Theorem Factorise The Polynomial X3 X2 4x 4 Studyrankersonline




6 Factor Graph Corresponding To The Factorisation Of F X 1 X 2 X Download Scientific Diagram




Factorising Quadratic Expressions 1




Ex 2 4 Q24c 𝑥3 𝑥2 4𝑥 4 Factorise




How To Factorize X 4 3x 2 2 Quora
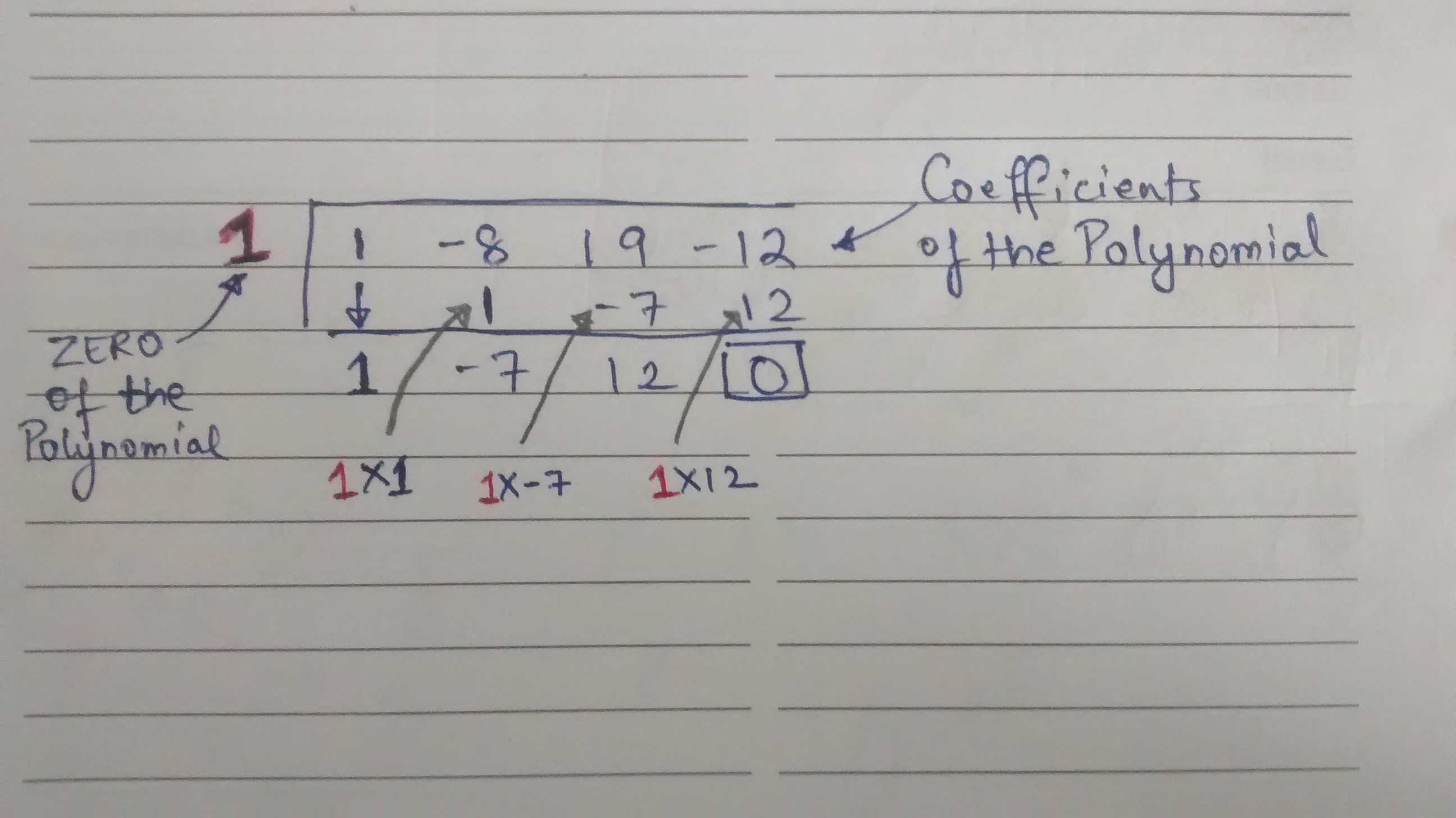



How Do You Factor X 3 8x 2 19x 12 Socratic



How To Factorize X 4 4 Quora




Factoring Special Binomials



Www Nhgs Co Uk Storage App Media Sixth Form Transition Work Maths Questions And Answers 1b 3 Solving Quadratic Equations Pdf




Factorize Each Of The Following Rational Expressions X 4 4 Ii X 4 4x 2 3




Factorise X X 1 X 2 X 3 4 Ellajetan




2 The Function F X X3 X2 4x 4 Crosses The Chegg Com



Www Nextgurukul In Questions Answers Forum Question Academic Factorise 2xx 4 2x 5x 3 253




Factoring X 4 Polynomials Completely Youtube




1 1 2 Xx 2 2x X 1 2 Factorise The Following 1 Gauthmath




Factorise X 1 X 2 X 3 X 4 3 Mathematics Topperlearning Com B0sdcrr
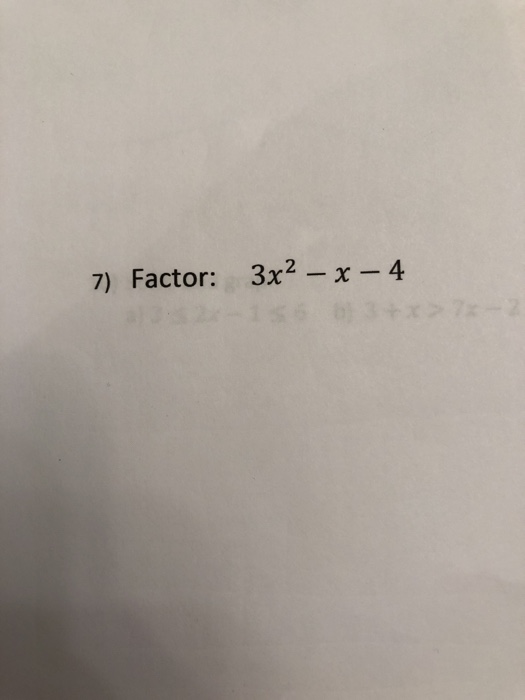



7 Factor 3x2 X 4 Chegg Com




Factoring By Grouping Solutions Examples Videos
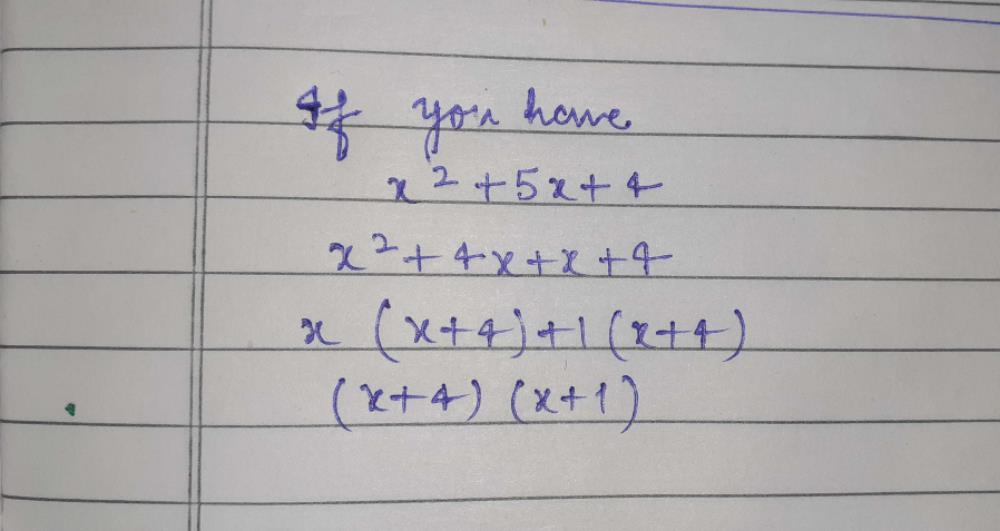



Factorise X2 5x 4 Edurev Class 10 Question



How To Factorize X 4 4 Quora




Factoring Special Binomials



Math Scene Equations Iii Lesson 2 Quadratic Equations




Factorise A X 4 4x 2 16 Ii X 4 4



Thedeanacademy Org Wp Content Uploads 02 Maths Y11 Solving Quadratics By Factorising Pdf




Starter Whats The Same And Whats Different X




Factorise X 4 4 4 X 4 1 By A 2 B 2 Brainly In



How Do You Divide X 3 X 2 4x 4 X 2 Using Polynomial Long Division Socratic



How To Factor 10 Steps With Pictures Instructables




Unit 8 Section 3 Common Factors Factorising




Factorise 3x 2 X 4 Maths Questions




Algebra Assessment Solutions Algebra And
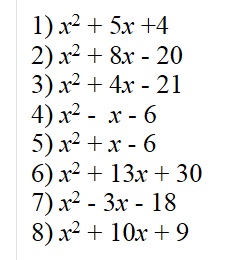



Algebra 6 Factorising Mathtec




Factorize X 4 16 Into Linear Polynomials Youtube




Completing The Square Video Khan Academy




Solve For X In This Complex Equation X 4 3x 2 4 0 Youtube




What Is The Factor Of X Power 4 4 Maths Factorisation Meritnation Com




How To Factorise A Polynomial By Splitting The Middle Term A Plus Topper




Factorise X X 1 X 2 X 3 4 Ellajetan




Sol 2 4 Factorization Discrete Mathematics
.png)



Factorise X4 4 X4 Maths Polynomials Meritnation Com




As Mathematics Algebra Graphical Solution Of Quadratic Equations



1




Factor 81a 4 25b 2 Factor X 2 25 Factor Chegg Com




How To Factor Math X 4 4x 3 2x 2 4x 1 Math Quora




Factoring Higher Degree Polynomials Video Khan Academy




Solved X Square 4 Y Square 4 X 4 Factorise It Self Study 365




Question Video Factorizing By Grouping Nagwa




Factor X 4 9 Youtube




X X 2 X 4 4x 8 Factorise This Maths Polynomials Meritnation Com




1 Expand Brackets 2 Factorise Ppt Download



0 件のコメント:
コメントを投稿